Diffraction data merging

Overview

Once all individual diffraction patterns have been processed, each reflection of each pattern is characterized by a duplet of (h,k), the crystallographic lattice index of the reflection. The integration step assigned an intensity (iobs) and an associated error estimation (sigiobs) to each reflection; a subsequent step used the tilt geometry to calculate the z* (zstar) value as well as its error estimation (sigmazstar).

The merge process is responsible for first combining reflections from the individual patterns and then discretizing the irregularly spaced reflections to obtain a full crystallographic dataset with reflections organized in (h,k,l) triplets. At this point, it is very useful to think of the combined data as they distribute into lattice lines- ultimately, it will be those lattice lines which will allow the z* to l discretization. Generally speaking, each diffraction pattern contributes to each lattice line, as explained in figure 1. The merge processing goes back and forth between the lattice line and individual pattern representation, and thus it is important to understand how they relate to each other.

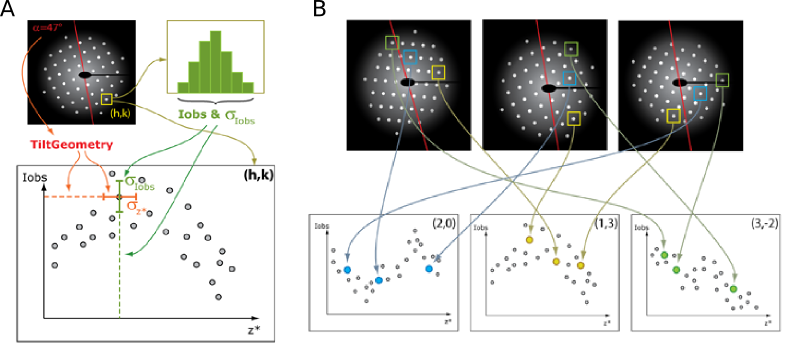
Figure 1: The relationship between diffraction patterns and lattice lines. (A) The contribution of a single diffraction pattern (top left) to a lattice line (bottom). A lattice line is a 2D plot, based on a particular (h,k) duplet. Its abscissa represents the z* value, which is based on the tilt geometry of the pattern. Its ordinate represents the intensity (iobs), which is determined during the integration step in the pattern processing. Estimated errors, both in x and y, play an important role in the merge processing. From the integration, an measure of uncertainty is obtained for the intensity (sigiobs). For estimating the z* error (sigmazstar), the uncertainty of the precise lattice vectors is used. (B)Each diffraction pattern (top row) will usually contribute to each lattice line (bottom row), as indicated with the three reflections at indices (2,0), (1,3) and (3,-2), in blue, yellow and green, respectively.

The merge process has four distinct steps. In the beginning, reflections from all datasets are pooled, and the crystallographic symmetry is applied. Then, a scaling algorithm takes account of the fact that each pattern is from an individual measurements, meaning that the integrated intensities cannot be just thrown together. Following this step is the tilt geometry refinement, which tweaks the z* values. Finally, the lattice line discretization models the scattered points of each lattice line as a continuous curve, and yields reference reflections at discretized values.

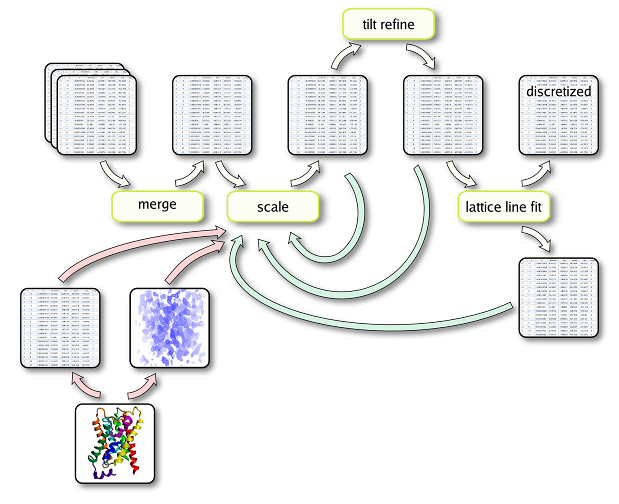
Figure 2: Merging overview

An overview over the merging process is given in figure 2 and a summary of this process from the perspective of a single lattice line is given in figure 3.

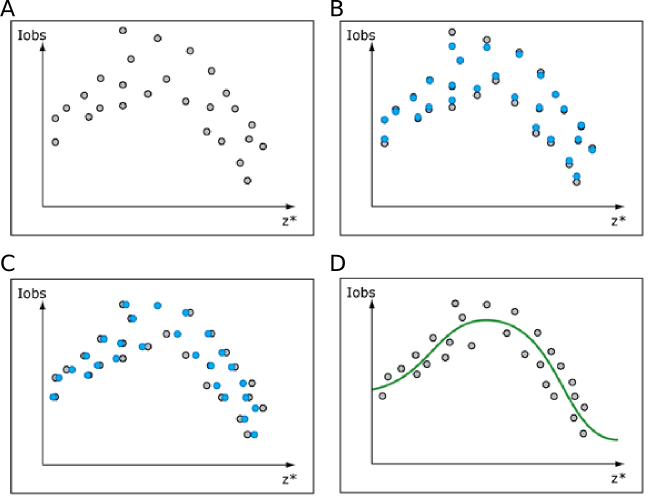
Figure 3: <strong>Figure 3: Merge processing steps as seen from the lattice line perspective.</strong> (A) First merge: scattering of lattice line values in both x- and y-direction. (B) Scaling: only Iobs are affected (y-axis). The change in the intensities (grey to blue points) may be different for each value, as they originate from different patterns. (C) Tilt geometry refinement: only z* values are affected (x-axis). (D) Lattice line fitting: the scaled and tilt-geometry-refined values are modeled by a curve, which then gives the discretized values.